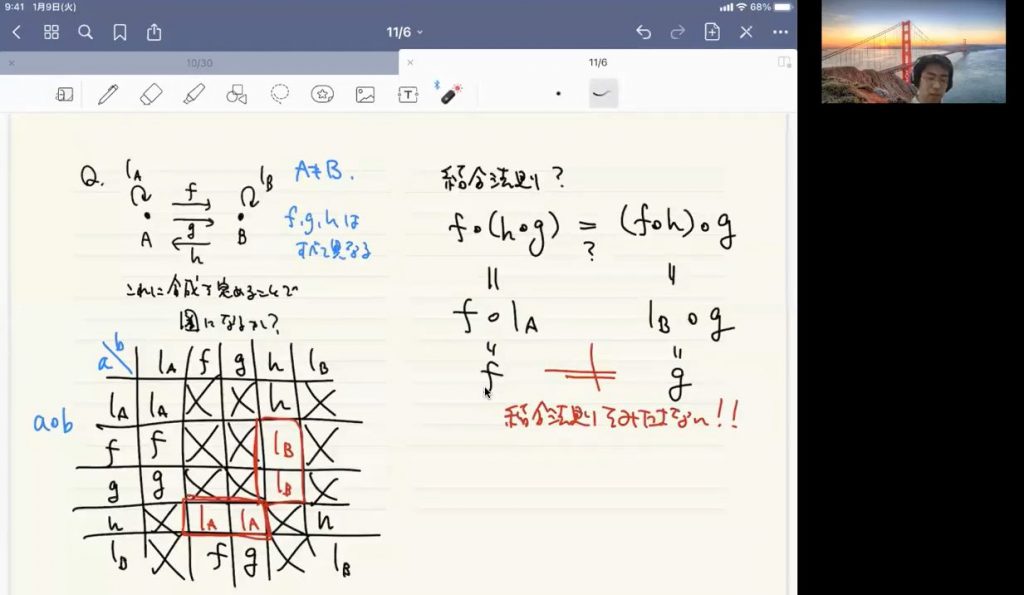
普遍性という概念を中心に圏論について紹介
この講座では、丸善出版から出版されている『ベーシック圏論』(T.レンスター著、斎藤恭司監修、土岡俊介訳)を教科書として、現代的な数学の広い範囲に関わる圏論について学びます。使用する教科書のサブタイトルに普遍性からの速習コースとあるように、この講座では「普遍性」という概念を中心にして圏論についての基本的概念をコンパクトに紹介します。
※アーカイブ講座の動画販売についてお申し込み受付中です。
数学講座
通常講座
Aアドバンス
アーカイブ講座(録画販売中)

この講座では、丸善出版から出版されている『ベーシック圏論』(T.レンスター著、斎藤恭司監修、土岡俊介訳)を教科書として、現代的な数学の広い範囲に関わる圏論について学びます。使用する教科書のサブタイトルに普遍性からの速習コースとあるように、この講座では「普遍性」という概念を中心にして圏論についての基本的概念をコンパクトに紹介します。
※アーカイブ講座の動画販売についてお申し込み受付中です。
この講座では、丸善出版から出版されている『ベーシック圏論』(T.レンスター著、斎藤恭司監修、土岡俊介訳)を教科書として、現代的な数学の広い範囲に関わる圏論について学びます。
「圏論は鳥の目で数学を俯瞰する」と教科書の序文にあります。圏論は、数学の様々な分野にわたって共通して現れるパターンを数学的に取り扱うための言語を提供します。また、圏論の考え方は、コンピュータ科学をはじめとする数学以外の分野でも利用されています。
使用する教科書のサブタイトルに普遍性からの速習コースとあるように、この講座では「普遍性」という概念を中心にして圏論についての基本的概念をコンパクトに紹介します。
圏論における中心的な概念である「普遍性」を簡単に説明します。例えば要素を一つしか持たない集合は「他の集合Xをどうとろうとも、Xからの写像がただ一つ存在する」という性質をもち、またそれによって特徴づけられます。つまり、集合たちの世界では「要素が一つしか持たない集合」を他の集合との関係によって記述できるのです。
このように、ある圏のある対象が他の対象とどう関係するかを記述する性質、いいかえるとある対象がある圏の中でどのような役割を果たすかを記述する性質のことを「普遍性」といいます。普遍性によれば、具体的な構成まで立ち入ることなくその対象を特徴づけることができます。この講座では、随伴、表現可能関手、極限という三つの見方を通して普遍性を学んでいきます。
圏論には数学の広い分野にわたって現れるパターンを抽象化するという特徴があり、そのためいろいろな数学的知識を持っているとより多くの具体例を理解できます。しかし全ての例を理解できるようになるのは難しく、教科書でも「すべての例を理解できるだけの数学的素養をもっていた学生はいなかったと思う.」とあるほどです。本講座では圏論の具体例を理解するために必要な知識についても時間の許す限り補足します。
この教科書では豊富な例や演習問題を通して基本的な概念を理解することができます。抽象的な数学を学ぶ上では様々な具体例について親しむとともに、数学的な事実を論理のみに基づいて証明していくことが必要です。演習問題については翻訳者による丁寧な解答がありますが、自分の書いたものが正しいのか間違っているのかというのはなかなか判断するのが難しいものです。この講座では、指定した演習問題を提出いただきそれ添削することで、数学的な証明を記述する能力を身につけていただくことを目指します。
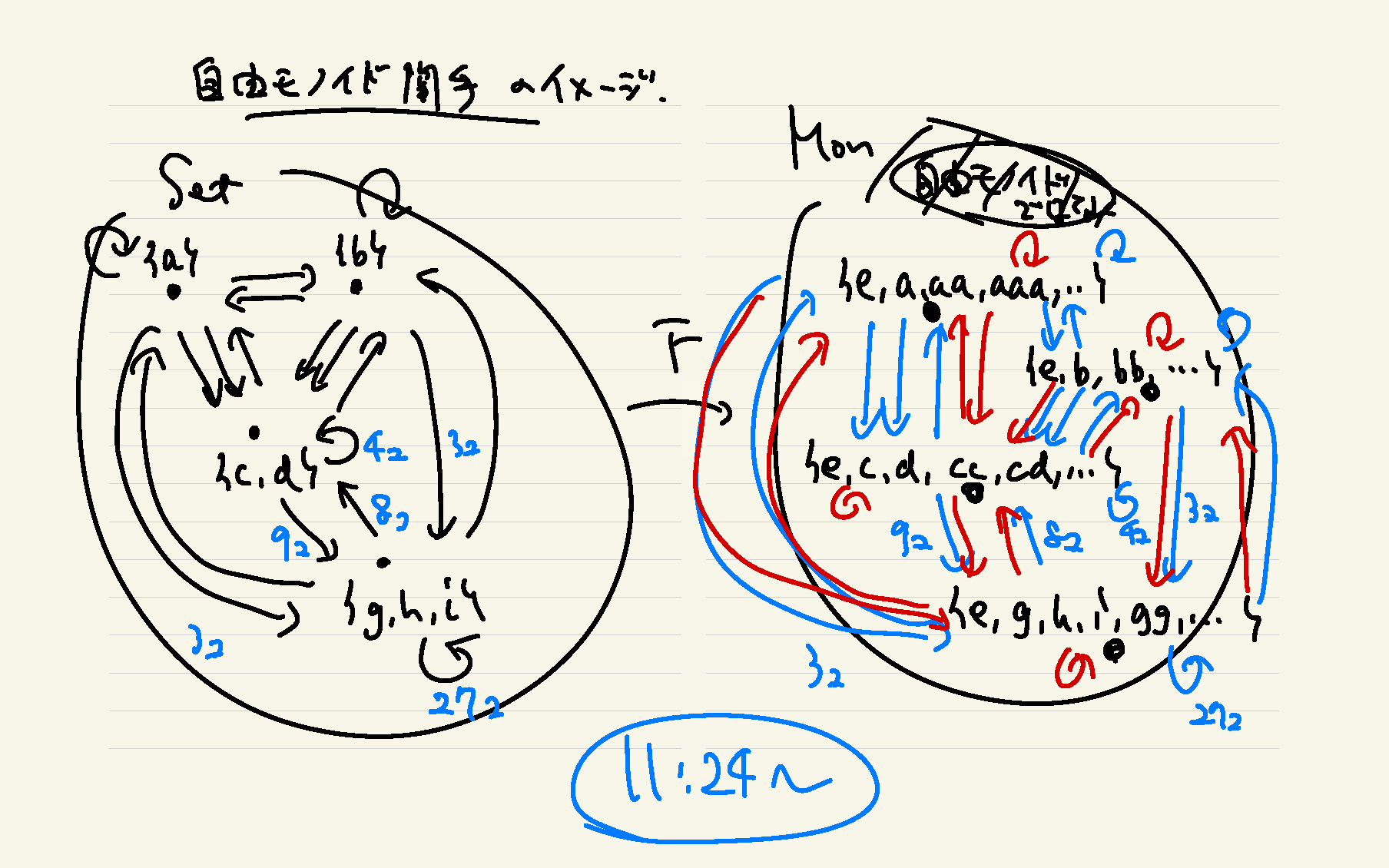
大学初年度までで習う程度の集合や論理について(例えば必要条件十分条件や量化子などの扱い)は既知とします。
数学的な事実を扱うための論理や集合についての取り扱いに慣れているとよいですが講義中にも随時補足します。(弊社講座論理学の基礎、弊社講座集合と位相の第2章まで、『論理と集合から始める数学の基礎』(日本評論社)など)
大学初年度で習う線形代数について知っているとよいです。(弊社講座線形代数 特別講義(加藤文元先生))
教科書の演習問題のうち講義中に指定した教科書の問題及び講師が作成した問題について、ご提出いただいた解答を添削いたします。
ここではまず圏や関手という概念について扱います。さらに自然変換についても扱います。この自然変換という概念こそが圏論の誕生の動機です。圏と圏を結びつけるものが関手であり、関手と関手を結びつけるものが自然変換です。この二段階の複雑な構造に慣れるのはなかなか難しいものですが、多くの具体例を通して馴染んでいきましょう。
普遍性への第一のアプローチとして随伴を扱います。随伴とは、二つの関手の間の特別な関係性のことです。随伴関手のいくつかの例とともに、随伴関手の三通りの定義を紹介しそれらの関係について扱うのがこの章の目的です。これまでにご存知の数学の中にも知らないうちに随伴やその帰結を扱っていることは多く、随伴について知ることで数学に現れるパターンを見つけやすくなります。
集合と関数は数学における基本的な概念です。この章ではこれらについて解説します。また、圏論においては、集合全体の圏や群全体の圏など、たくさんのものの集まりのなす圏を考えます。このようなたくさんのものの集まりは、集合論では扱いに注意が必要なものです。その点についても簡単に紹介します。
普遍性への第二のアプローチとして表現可能関手について扱うのがこの章のテーマです。冒頭に述べた一点集合の他の集合との間の写像による普遍性の記述は、この表現可能関手の考え方を用いたものです。つまり、ある特定の対象から他の対象を見るという考え方を定式化したものが表現可能関手です。また、有名な米田の補題についてもこの章で扱います。
普遍性への第三のアプローチとして極限と余極限について扱うのがこの章です。様々な数学的対象の構成方法は極限や余極限として理解することができます。自然数の最小公倍数や最大公約数、集合の直和や直積といった概念はその例です。この章では極限や余極限についてのたくさんの例を紹介します。
ここまでみてきた普遍性についての三つの概念、随伴、表現可能関手、極限の関係について扱います。またそれを利用して特に前層圏の性質について見ていきます。
| 講座名 | ベーシック圏論 |
|---|---|
| 担当講師 | |
| 開講スケジュール |
土曜クラス : 10:00-12:00
2021年10月16日~2022年3月5日
12月25日、1月1日土曜日は休講です。 |
| 受講方法 |
Zoomによるオンライン講座 |
| 教科書 | T.レンスター著、斎藤恭司監修、土岡俊介訳『ベーシック圏論』(丸善出版) ※著作権の関係上、お持ちでない場合は必ずご購入いただくようお願いいたします。著者及び出版社には、教科書として使用する許可を得ておりますが、本講座とは無関係です。 本講座に関しては弊社へのみお問い合わせください。 |
| 受講料 | 税込19,500円/月 |
| お支払い方法 |
クレジットカード決済
お手続き方法は「ご利用ガイド」をご確認ください。
|
| 準備物 | 筆記用具、教科書 |
下記のボタンを押すと該当する集団講座のチケットをご購入いただけます。
※ボタンを押すと、stripeの決済ページへ遷移します。

| 1ヶ月 | 2ヶ月 | 5ヶ月一括 |
|---|---|---|
2020年前期分よりオンライン授業を録画し、授業の録画販売(アーカイブ販売)を行っております。



アーカイブ講座の動画購入をご検討いただく場合は、下記についてご確認をお願いいたします。
本講座は開講中の講座はございません。
アーカイブ講座(録画購入)にてご受講いただけます。
アーカイブ講座(録画購入)のお申し込みはこちら
| 講座名 | 動画内容 | 講師名 | 受講料 |
|---|---|---|---|
| ベーシック圏論 2021年後期 |
全19回 (各120分) |
梅崎 直也 | 97,500円 (19,500円/月) |
年度別 講座情報
| 年度 | 講座情報 |
|---|---|
| ー | 本講座は2021年後期のみの開講です。 |
講座のお申し込み・ご相談は
気軽にお問い合わせください。