
グレブナー基底の背景とその応用について解説する
複雑な連立代数方程式をある程度簡単な形にしたり、計算機で扱いやすい形にする方法の一つとしてグレブナー基底理論があります。
本講義ではこのようなグレブナー基底について、背景にある数学的事実や計算方法、その応用などを、グレブナー基底研究を専門とする講師が解説します。
※アーカイブ講座の動画販売についてお申し込み受付中です。
数学講座
無料公開講座
スポット講座
Aアドバンス
アーカイブ講座(録画販売中)

複雑な連立代数方程式をある程度簡単な形にしたり、計算機で扱いやすい形にする方法の一つとしてグレブナー基底理論があります。
本講義ではこのようなグレブナー基底について、背景にある数学的事実や計算方法、その応用などを、グレブナー基底研究を専門とする講師が解説します。
※アーカイブ講座の動画販売についてお申し込み受付中です。
この世には様々な方程式がありますが、その中で最も基本的な方程式は多項式による方程式です。多項式による方程式を代数方程式といいます。
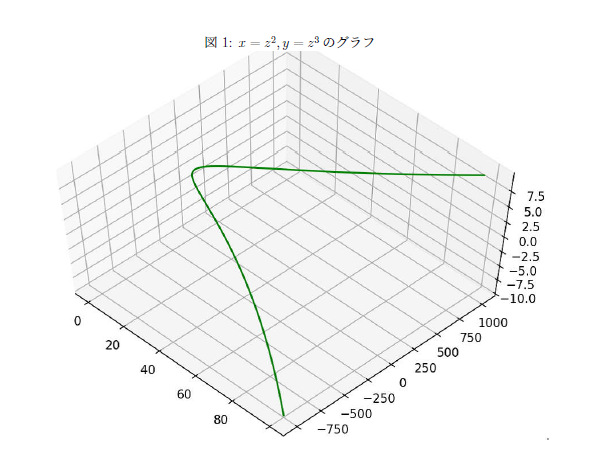
例えば、 \(y=x^2\) など、放物線を表す方程式も代数方程式の一つです。また、代数方程式 \(x^2=2\) の正の解は「面積が2である正方形の辺の長さ」となります。
このように代数方程式は基本的であるがゆえに様々な事柄を表すことができます。しかしながら、下記のように変数を増やしたり連立させたりすると、その様子は一気に複雑化していきます。
例えば、上記の連立方程式に関するグレブナー基底を求めてみると下記のようになります。
本講義ではこのようなグレブナー基底について、背景にある数学的事実や計算方法、その応用などを、グレブナー基底研究を専門とする講師が解説します。
すうがくぶんかのオリジナルテキスト
デジタルデータにてお送りいたします
高校数学までの数学、特に関数や、集合と論理について基本的な知識(参考:大人のための高校数学、論理学の基礎)
まずはグレブナー基底を計算して実物を観察してみましょう。無料の数式処理システムであるSageやRisa/Asirを使って計算のデモンストレーションを行います。Sageはブラウザ上で動かす事もできますので、とりあえず計算してみながら受講することができます。(参考: SageMathCell, CoCalc)
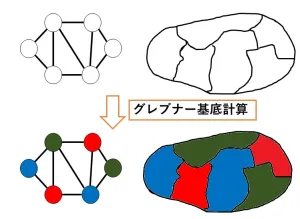
また応用の一つとして、グラフの塗り分け問題の一つである三彩色問題:「結ばれている頂点を同じ色で塗らないように、各頂点を三色で塗り分けよ」について、グレブナー基底を使った求解法を紹介します。
グレブナー基底の定式化には多項式環のイデアルと項順序への理解が必要となります。まずは多項式環のイデアルや項順序のアイデアを説明し、どのようにグレブナー基底が定式化されるかを紹介します。
グレブナー基底理論の最大の応用として、抽象的な数学の概念をコンピューターで実現・計算する方法を研究する計算数学との関わりがあります。
本講義ではその実例として、代数方程式が定める図形の次元について、グレブナー基底を用いた計算方法を紹介します。
グレブナー基底は求まれば非常に強力ですが、一方で原理的な計算困難性があることも紹介します。
半径1の円 \(x^2+y^2=1\) のように、代数方程式が定める図形を代数多様体といい、代数多様体を調べる学問を代数幾何学といいます。
本講義の最後では代数幾何学とグレブナー基底理論の関わりを紹介します。
そのほか、グレブナー基底を用いた研究にどのようなものがあるか、講演者の知る限り紹介します。
| 講座名 | 【無料公開講座 ’21】グレブナー基底入門 |
|---|---|
| 担当講師 |
神戸 祐太
|
| 開講スケジュール |
2021年12月26日(日)全1回 |
| 受講方法 |
Zoomによるオンライン講座 |
| 教科書 | すうがくぶんかのオリジナルテキスト |
| 受講料 | 無料 |
| 準備物 | 筆記用具 |
2020年前期分よりオンライン授業を録画し、授業の録画販売(アーカイブ販売)を行っております。



アーカイブ講座の動画購入をご検討いただく場合は、下記についてご確認をお願いいたします。
本講座は開講中の講座はございません。
アーカイブ講座(録画購入)にてご受講いただけます。
アーカイブ講座(録画購入)のお申し込みはこちら
| 講座名 | 動画内容 | 講師名 | 受講料 |
|---|---|---|---|
| 【無料公開講座 ’21】グレブナー基底入門 2021年後期 |
全1回 |
神戸 祐太 |
無料 |
年度別 講座情報
| 年度 | 講座情報 |
|---|---|
| ー | 本講座は2021年後期のみの開講です。 |
講座のお申し込み・ご相談は
気軽にお問い合わせください。