ルベーグ積分とはどんな積分なのか
本講座はリーマン積分の復習から始め,メインテーマであるルベーグ積分とどのように違うかを説明します.その際,どのような道筋をたどってルベーグ積分を考えていくのかも説明します.
その後,ルベーグ積分の理論をイチから説明し,種々の性質を数学的にきちんと扱っていきます.
※アーカイブ講座の動画販売についてお申し込み受付中です。
数学講座
通常講座
Aアドバンス
アーカイブ講座(録画販売中)

本講座はリーマン積分の復習から始め,メインテーマであるルベーグ積分とどのように違うかを説明します.その際,どのような道筋をたどってルベーグ積分を考えていくのかも説明します.
その後,ルベーグ積分の理論をイチから説明し,種々の性質を数学的にきちんと扱っていきます.
※アーカイブ講座の動画販売についてお申し込み受付中です。
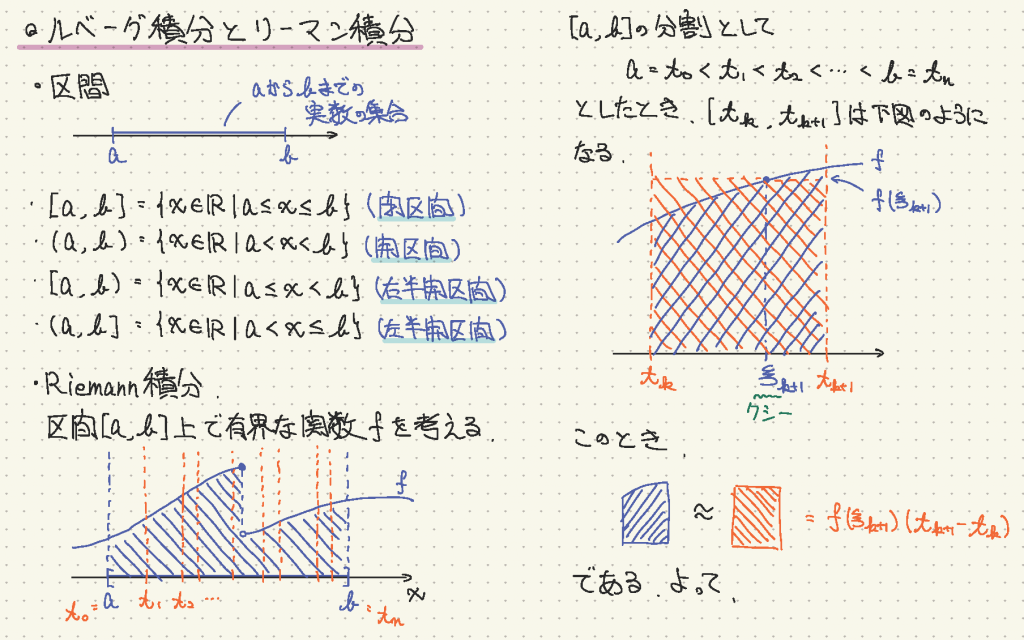
多くの理系大学生は1年でリーマン(Riemann)積分を学びます. リーマン積分は定義が単純で直感的に理解しやすい積分となっていますが,専門的な内容になってくるとリーマン積分では扱いづらくなることも少なくありません.そこで,より数学的に扱いやすい積分としてルベーグ(Lebesgue) 積分があります.
本講座では「リーマン積分に対してルベーグ積分がどのような積分なのか」というイメージから始め,ルベーグ積分の理論をイチから説明し,種々の性質を数学的にきちんと扱っていきます.
本講座では「リーマン積分に対してルベーグ積分がどのような積分なのか」というイメージから始め,ルベーグ積分の理論をイチから説明し,種々の性質を数学的にきちんと扱っていきます.
ルベーグ積分を理解するためには集合論と微分積分学の基本的な知識を必要としますが,これらは授業内でも説明する予定です (テキストでも説明されています).
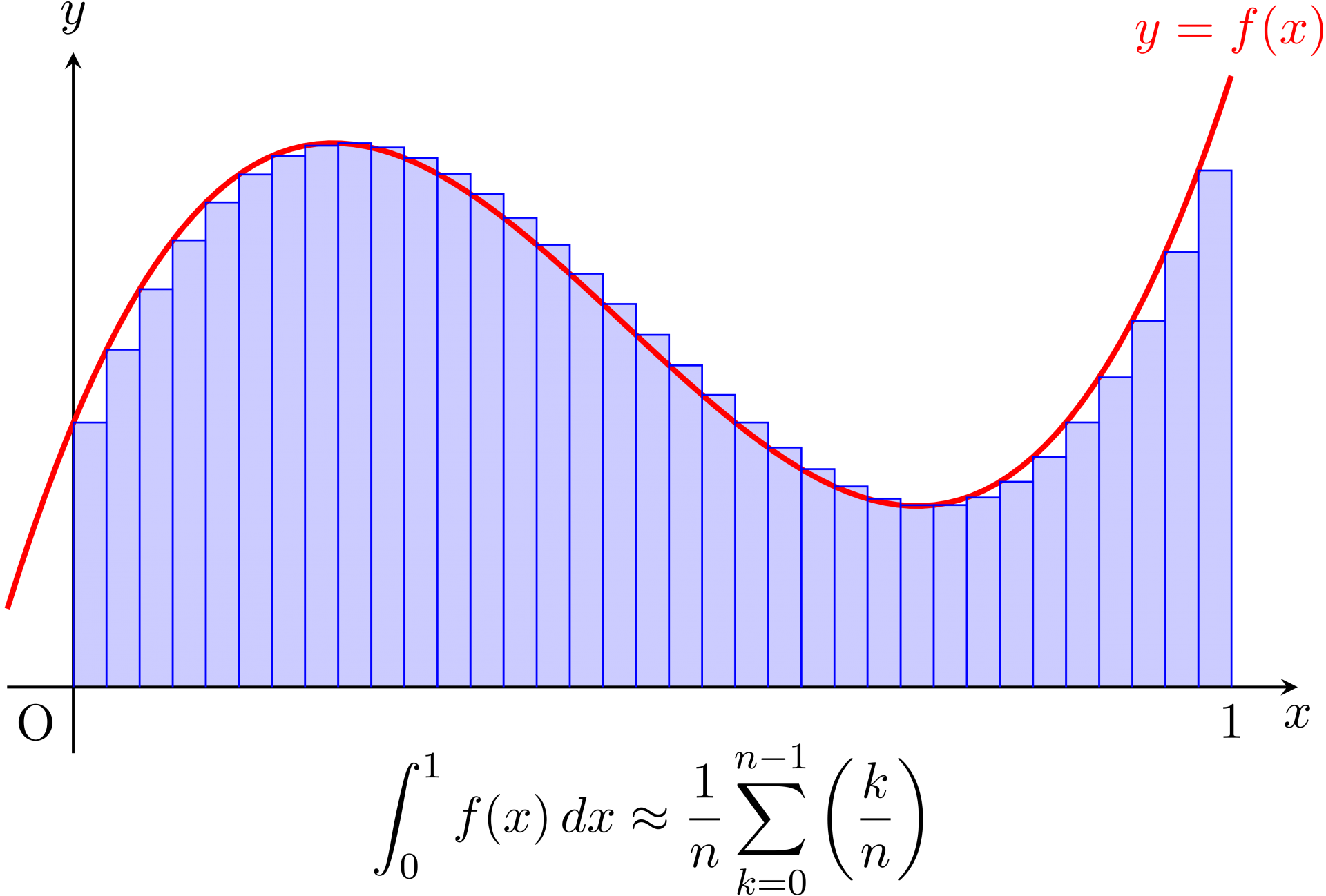
高校数学では区分求積法という考え方の求積法を学びます.しかし,区分求積法は少々特別な求積法のため連続関数を主に扱う高校数学では通用するものの,連続関数以外も対象となるより広い積分においては良い方法とは言えません.リーマン積分は区分求積法の考え方をより広い関数にも適切に定義できるように考えたものとなっています.
本講座はリーマン積分の復習から始め,本講座メインテーマであるルベーグ積分とどのように違うかを説明します.その際,本講座ではどのような道筋をたどってルベーグ積分を考えていくのかも説明します.

ルベーグ積分は測度論というより広い分野に属します.測度論は「集合の『長さ』や『頻度』」といった「集合の『元(要素) の量』」を測る分野で,ルベーグ積分の他に確率論も測度論に属します.
このためルベーグ積分を学ぶためには集合についてよく知っている必要があります.このセクションではルベーグ積分を扱う上で重要な集合論の基礎知識をここで解説します.
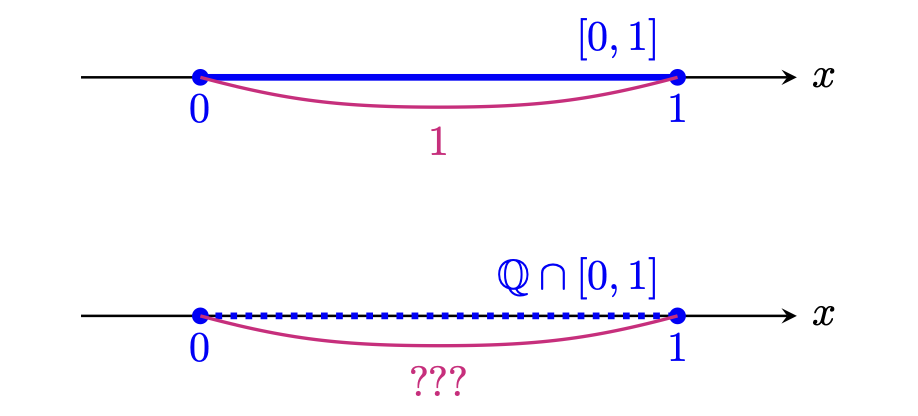
このように,ルベーグ積分においては「集合の長さ」を考えることが重要です.例えば「区間[0, 1] の長さ」を1 といえることは直感的に理解できますが,「区間[0, 1] 上の有理数の集合の長さ」はどうなるでしょうか?
日常の感覚では有理数の集合という「まばらな集合」に対して「長さ」を考えることは難しいですが,数学ではこのような集合にも「長さ」に相当するものを考えることができます.詳しく言えば,この「長さ」はルベーグ測度というものを用いて考えることになります.その際,どんな集合でもルベーグ測度を用いて「長さ」を測ることができるわけではなく,「長さ」を測ることができる集合として可測集合を定義します.この可測集合とルベーグ測度はルベーグ積分のベースになる非常に重要なところで,このセクションでは「可測集合とルベーグ測度をどのように定めるか」というところを測度論の考え方も踏まえつつ説明します.
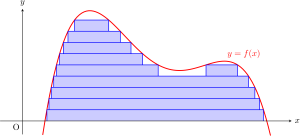
リーマン積分は「縦切り」によって面積を求めようという考え方をしていた一方で,ルベーグ積分は「横切り」によって面積を求めようというアプローチを採ります.
有界閉区間においては,リーマン積分可能な関数は必ずルベーグ積分可能であることが知られており,この意味でルベーグ積分はリーマン積分の拡張であるといえます.このセクションでは可測関数を定義して基本的な性質を述べたあと,ルベーグ積分の定義と基本性質を説明します.
解析学(微分と積分を主に扱う分野) では極限と積分の順序交換をしたい場面はよくあり, 極限と積分の順序交換ができることを項別積分可能であるといいます.
ルベーグ積分での項別積分可能であるための条件を述べた述べた定理をルベーグの収束定理といいます. この条件はリーマン積分よりかなり扱いやすいものとなっており,これがルベーグ積分を学ぶ1つの大きなメリットとなっています.このセクションではルベーグの収束定理の証明を目指し,具体的にルベーグの収束定理の使い方をみます.
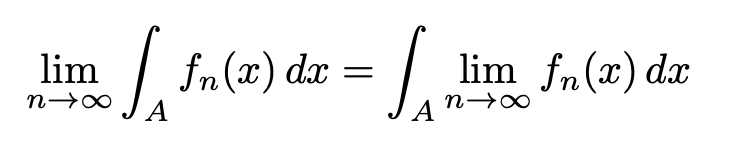
| 講座名 | ルベーグ積分入門 |
|---|---|
| 担当講師 | |
| 開講スケジュール |
日曜クラス : 10:00-12:00
2022年10月9日~2023年2月26日
12月25日、1月1日日曜日は休講です。 |
| 受講方法 |
Zoomによるオンライン講座 |
| 教科書 | 吉田 洋一著「ルベグ積分入門」(筑摩書房) ※著作権の関係上、お持ちでない場合は必ずご購入いただくようお願いいたします。著者及び出版社には、教科書として使用する許可を得ておりますが、本講座とは無関係です。 本講座に関しては弊社へのみお問い合わせください。 |
| 受講料 | 税込19,500円/月 |
| お支払い方法 |
クレジットカード支払いは本ページ下部「受講料のお支払いについて」よりお願いいたします。 |
| 準備物 | ・筆記用具 |
下記のボタンを押すと該当する集団講座のチケットをご購入いただけます。
※ボタンを押すと、stripeの決済ページへ遷移します。

| 1ヶ月 | 2ヶ月 | 5ヶ月一括 |
|---|---|---|
2020年前期分よりオンライン授業を録画し、授業の録画販売(アーカイブ販売)を行っております。



アーカイブ講座の動画購入をご検討いただく場合は、下記についてご確認をお願いいたします。
本講座は開講中の講座はございません。
アーカイブ講座(録画購入)にてご受講いただけます。
アーカイブ講座(録画購入)のお申し込みはこちら
| 講座名 | 動画内容 | 講師名 | 受講料 |
|---|---|---|---|
| ルベーグ積分入門 2022年後期 |
全19回 (各120分) |
山本 拓人 | 19,500円/月(97,500円/5ヶ月一括) |
| ルベーグ積分入門 2021年後期 |
全19回 (各120分) |
山本 拓人 | 19,500円/月(97,500円/5ヶ月一括) |
年度別 講座情報
| 年度 | 講座情報 |
|---|---|
| 全年度共通 | 本講座はカリキュラム等について全年度共通です。 |
講座のお申し込み・ご相談は
気軽にお問い合わせください。