最尤推定を軸に機械学習を学ぶ
機械学習に用いられる多変量解析の手法には、様々な場面で数理統計の考え方や知識が役に立っています。なかでも大切なのは最尤推定です。
そこでこの講座では、古典から最先端の手法まで幅広いトピックを最尤推定を軸に解説します。実務で機械学習を使っている方から趣味で数理統計を学んでいる方まで、幅広い方の受講をお待ちしております。
※アーカイブ講座の動画販売についてお申し込み受付中です。
統計・機械学習講座
通常講座
Aアドバンス
アーカイブ講座(録画販売中)

機械学習に用いられる多変量解析の手法には、様々な場面で数理統計の考え方や知識が役に立っています。なかでも大切なのは最尤推定です。
そこでこの講座では、古典から最先端の手法まで幅広いトピックを最尤推定を軸に解説します。実務で機械学習を使っている方から趣味で数理統計を学んでいる方まで、幅広い方の受講をお待ちしております。
※アーカイブ講座の動画販売についてお申し込み受付中です。
この講座は、機械学習に用いられる多変量解析の手法を、その仕組みからじっくりと学ぶ講義です。古典から最先端の手法まで幅広いトピックを主に「最尤推定」を軸として解説します。数理統計学の知識があると望ましいですが、必ずしも事前に受講しておく必要はありません。最尤推定を含め、必要な知識は講座内で全て説明を行います。
扱うトピックは以下のとおりです。
– ロジスティック回帰モデル
– 混合正規分布のEM-algorthmによるクラスタリング
– マハラノビス距離・距離学習
– ロバスト回帰分析(外れ値を含むデータに対する回帰分析)
– PU Learning / PConf Learning
また各トピックで、その手法のイメージを掴み、理解しやすくするように、R言語またはPython言語を用いたデモを実施します。統計・機械学習を使っている方で手法の仕組みを数理的に理解できるようになりたい方から、数理統計を趣味で楽しんでいる方まで、幅広い方のご参加をお待ちしております。


すうがくぶんかのオリジナルテキスト
デジタルデータ(PDF)をメール添付にてお送りいたします
・最尤推定を通して機械学習に用いられる多変量解析手法の仕組みを理解できるようになる
・数理統計的な考え方ができるようになる
・高校数学で学ぶ微分積分の計算
最尤推定を復習し、機械学習の分類器のなかで最も有名なロジスティック回帰モデルを最尤推定の文脈で解説します。この講義を通して、ロジスティック回帰について深く理解できるだけでなく、数理統計学で学んだ最尤推定が機械学習モデルに応用される様子がわかると思います。
ロジスティック回帰は基礎から学び直してみると「あれ?そんな手法だったんだ」という声もいただくので、色々と勉強になることをお話しできるのではないかと思います。
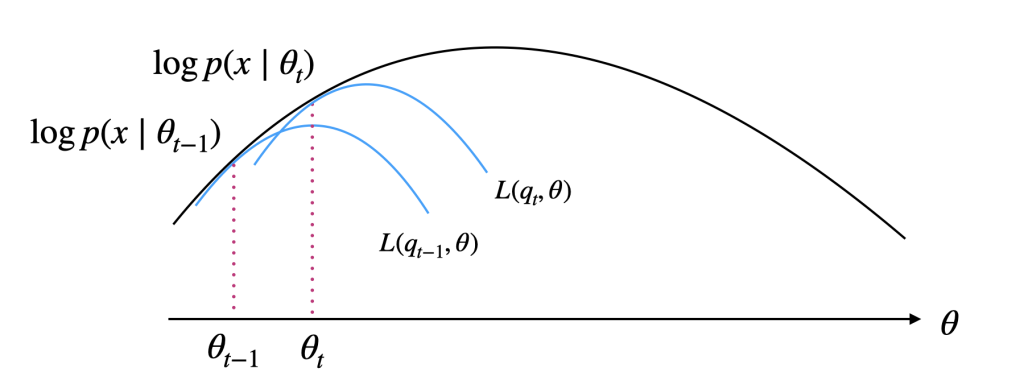
最尤推定量の数値計算の方法として有名でありながら理解が難しいことでも知られるEM-algorithmを解説し、混合正規分布によるクラスタリングに応用します。k-means法の発展的な手法として、手法自体が面白いトピックだと思います。
マハラノビス距離は重要な場面で応用されることも多いので、理解したいという方も多いのではないでしょうか。
マハラノビス距離は苦手な方も多いので、定義に必要な二次形式とそのグラフの関係から丁寧に解説します。マハラノビス距離の応用といえば異常検知・判別分析・距離学習が代表的だと思いますが、今回は距離学習の文脈で紹介し、第3期の最終回には深層距離学習に関する簡単な紹介もしたいと思います。
最尤推定を拡張したM推定を導入し、外れ値を含むデータに対する対処法の一例を解説します。最初は概念に慣れるために平均値や尺度のM推定から始めますが、最終的には回帰分析にM推定を応用します。時間に余裕があれば、発展的な手法であるMM推定についても解説します。
外れ値に対応する手法はなかなか勉強する機会がないと思うので、この機に一緒に勉強しましょう。
解約予測のような問題では、「まだ解約していないだけですでに意思はある」ような人がいる可能性があります。これは解約ラベルは確定的だが、未解約ラベルにはむしろ確定的なラベルを振らない方が良い可能性を示唆しているかもしれません。このような場合に役に立つのがPU Learning、PConf Learningです。
機械学習課題が単に回帰や分類といった有名なものだけではないこと、そしてこのような新しいフレームワークを解決する際にも数理統計の考え方が役に立っていることを、この発展的な話題を例に感じてもらえると嬉しいです。
| 講座名 | 続・数理統計学【多変量解析の数理】 |
|---|---|
| 担当講師 | |
| 開講スケジュール |
土曜クラス : 13:30-15:30
2025年04月12日~2025年09月06日 毎週土曜日
2025年05月03日, 2025年08月16日 は休講です。 第1期:2025/04/12, 19, 26, 05/10 支払い期日:04/19
第2期:2025/05/17, 24, 31, 06/07 支払い期日:05/16
第3期:2025/06/14, 21, 28, 07/05 支払い期日:06/13
第4期:2025/07/12, 19, 26, 08/02 支払い期日:07/11
第5期:2025/08/09, 23, 30, 09/06 支払い期日:08/08
|
| 受講方法 |
Zoomによるオンライン講座 授業は録画されます。録画(アーカイブ動画)は授業終了から5年間オンラインにて繰り返しご視聴いただけます。(ダウンロード不可) 詳細はこちらのページをご確認ください。 |
| 教科書 | すうがくぶんかのオリジナルテキスト |
| 受講料 |
|
| お支払い方法 |
クレジットカード支払いは本ページ下部「受講料のお支払いについて」よりお願いいたします。 ※はじめて本講座をご受講いただく方はお申し込み・お問い合わせフォームよりご連絡ください。事務局より受講に関するご案内やお支払い方法の詳細をお知らせいたします。 |
| 準備物 | 筆記用具、必須ではありませんがR, PythonをインストールしたPCがあると理解が深まります |
下記のボタンを押すと該当する集団講座のチケットをご購入いただけます。
ご都合にあわせて「1期分ずつ」「1期分×2回(2期分まとめ払い)」「全5期分一括払い」のいずれかをお選びください。
※ボタンを押すと、stripeの決済ページへ遷移します。
※はじめて本講座をご受講いただく方はこちらのお申し込み・お問い合わせフォームよりご連絡ください。事務局より受講に関するご案内やお支払い方法の詳細をお知らせいたします。

| 1期分 | 1期分×2回(2期分まとめ払い) | 全5期分一括払い |
|---|---|---|
2020年前期分よりオンライン授業を録画し、授業の録画販売(アーカイブ販売)を行っております。



アーカイブ講座の動画購入をご検討いただく場合は、下記についてご確認をお願いいたします。
はじめて本講座をご受講いただく方は【ご利用ガイド】をご確認の上、お申し込み・お問い合わせフォームよりご連絡ください。
現在開講中および開講予定の講座はございません。
アーカイブ講座(録画購入)にてご受講いただけます。
アーカイブ講座(録画購入)をご希望の場合はこちらからお申込みください。
| 講座名 | 動画内容 | 講師名 | 受講料 |
|---|---|---|---|
| 続・数理統計学【多変量解析の数理】 2025年前期 |
全20回(各120分) | 内場 崇之 | ¥24,500/期(¥122,500/全5期一括払い) |
| 続・数理統計学【多変量解析の数理】 2022年前期 |
全19回 (各120分) |
井汲 景太 | ¥24,500/期(¥122,500/全5期一括払い) |
| 続・数理統計学【多変量解析の数理】 2021年後期 |
全19回 (各120分) |
井汲 景太 | ¥24,500/期(¥122,500/全5期一括払い) |
| 続・数理統計学【多変量解析の数理】 2021年前期 |
全19回 (各120分) |
内場 崇之 | ¥24,500/期(¥122,500/全5期一括払い) |
年度別 講座情報
| 年度 | 講座情報 |
|---|---|
| 2021年前期・後期、2022年前期 | 松井秀俊/小泉和之著『統計モデルと推測』講談社サイエンティフィクを教科書として使用します。 |
講座のお申し込み・ご相談は
気軽にお問い合わせください。