最尤推定を軸に機械学習を学ぶ
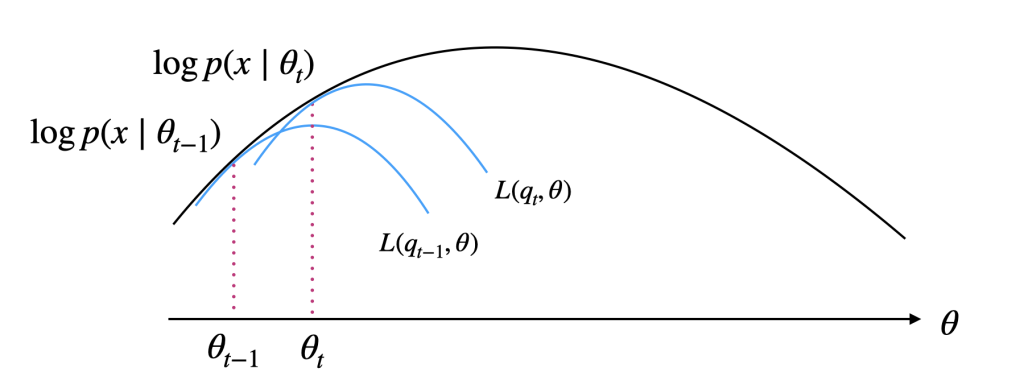
機械学習に用いられる多変量解析の手法には、様々な場面で数理統計の考え方や知識が役に立っています。なかでも大切なのは最尤推定です。
そこでこの講座では、古典から最先端の手法まで幅広いトピックを最尤推定を軸に解説します。実務で機械学習を使っている方から趣味で数理統計を学んでいる方まで、幅広い方の受講をお待ちしております。
※2025年前期(4月-9月)からのご受講についてお申し込み受付中です。アーカイブ視聴による参加、途中参加も可能です。
※アーカイブ講座の動画販売についてお申し込み受付中です。















