Pythonで学ぶ最適化問題

2021年度8月開講講座の録画販売についてお申込受付中です。

講座の概要

資源の配分や配送経路、販売価格などを与えられた条件の中で最も効率よく決めたい。最適化はこのような問題を解決するための数学的な手段を与えます。

この講座では、最適化の考え方や基礎的な理論について解説していきます。

また最適化の計算を実行するためにはコンピュータの力も不可欠です。理論の解説と並行してpythonによる実装も解説します。

最適化問題がどのような問題かを次のような例題を用いて紹介します。

例題

3種類の製品X,Y,Zを作っている。この製品を作るための材料はA,B,Cの3種類で、各製品を単位量作るために使う材料の量と利益をまとめると次の表のようになる。

材料A,B,Cはそれぞれ80,60,70ずつ用意してあるとするとき、各製品をどれだけ作れば利益が最も大きくなるか。

製品Xの利益が最も大きいことからXをたくさん作りたいところですが、材料をたくさん消費してしまうため作れる量は少なくなります。一方でYは材料はあまり必要としないのでたくさん作ることができるが利益は小さいです。Zはその中間といえます。このX, Y, Zを材料の制約のもとで最も利益を大きくするように生産する方法を求めるのが最適化問題です。

このように、様々な可能性の中から最も良いものを見つけ出すための数学的な手法を紹介しPythonによる実装を行うのがこの講座の目標です。

受講にあたって

受講にあたって役に立つ知識
高校数学1A, 2B, 3の範囲まで

カリキュラム

1. 最適化の概要

まず典型的な問題を通してこの講座のテーマである最適化問題とはどのような問題であるか、それをどのような手法で解決するのか紹介します。また、最適化はその数学的な性質によって線形最適化、非線形最適化、凸最適化など様々な種類に分類されています。これらの分類についても概要を説明します。

2. 線形最適化

目的関数、制約条件が1次式で与えられる最適化問題を線形最適化といいます。様々な最適化問題の中でも基本的なもので、厳密に最適値を求めることができます。不等式条件を扱うためのスラック変数の考え方も説明します。

解法として単体法や内点法などが知られており、この講義では特に単体法のアルゴリズムについて詳しく解説します。線形最適化は基本ではありますが適用できる状況は多くとても有用です。線形最適化の適用例としてスケジューリング問題を扱います。

3. 非線型最適化

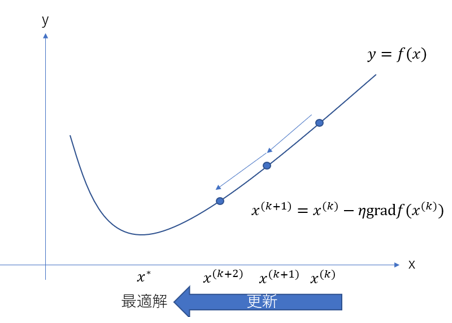
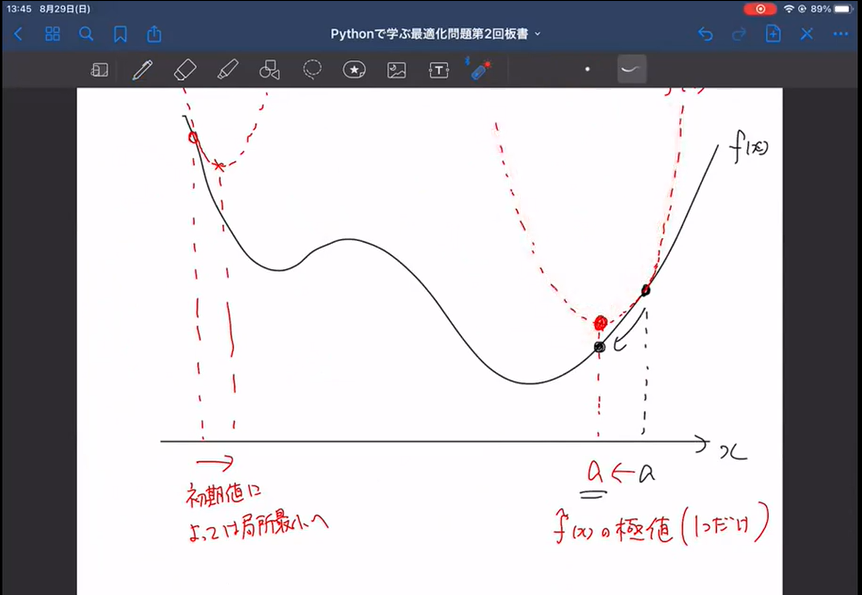
一般に目的関数や制約条件が1次式とは限らない最適化問題についての最適化手法について解説します。このような場合にはしばしば厳密に最適値を求めるのが困難です。そのため、近似的な手法を用います。具体的な方法として勾配法とNewton法Levenberg-Marquardt法を紹介します。いずれも微分を用いた近似解法で、目的関数によってはうまく近似できない場合があります。このような例についても具体的な問題を通して解説します。

4. その他のテーマ

ここまでで触れられなかった話題について紹介します。
最短経路問題(Dijkstra法)、双対問題、時間が許せば凸最適化について簡単な紹介をします。

お申込み

お申し込みは、お申込フォームからお願いします。
※お手数ですが、件名について『Pythonで学ぶ最適化問題』を選択のうえ送信をお願いします。

お申込