計算機実験で直観的に学ぼう！

マルコフ連鎖モンテカルロ法を中心に計算統計を第一線で研究してきた伊庭幸人先生に、計算機実験を通した確率の入門講義、そしてモンテカルロ法やマルコフ連鎖モンテカルロ法の入門講義を行なっていただきます。

伊庭先生の講義には、どんな話題であってもハッとするような解説も多く、皆さんも慣れ親しんだ知識であっても、これまで理解できなかった概念であっても、きっと何かしらの発見があると思います。

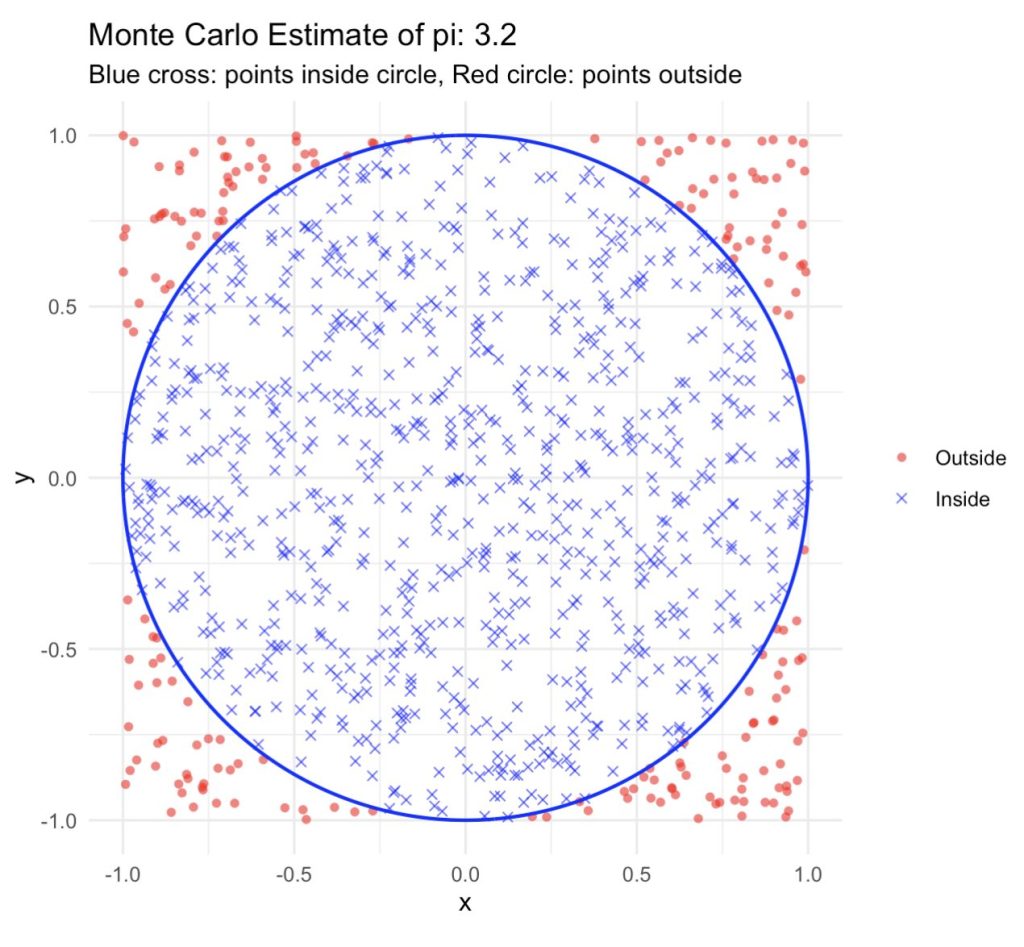
また今回は、中心極限定理といった確率・統計の基本的な話題から円の面積や球の体積といったモンテカルロ法、マルコフ連鎖モンテカルロ法まで、計算機の力を借りて様々な話題に触れていただけます。それだけに楽しく学べる講義です。ぜひこ受講ください。