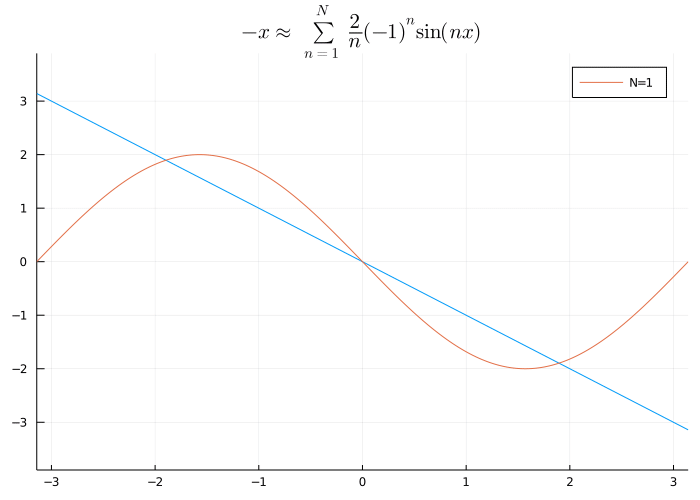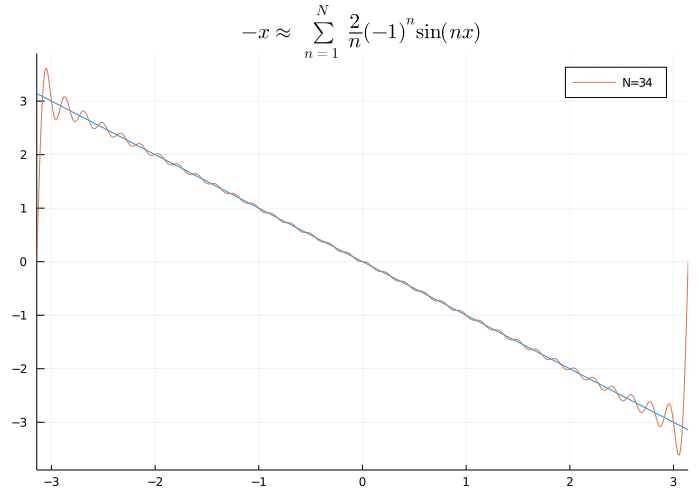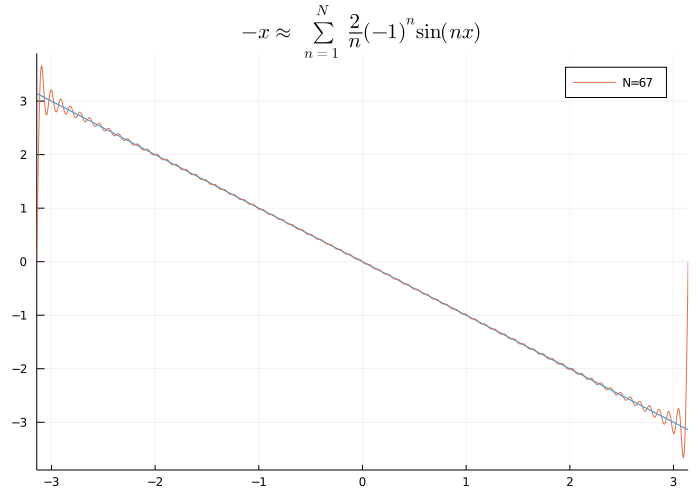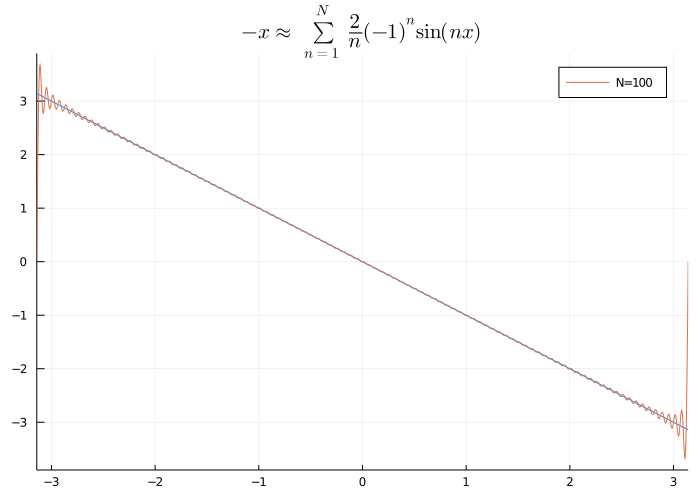
例題を中心にフーリエ解析・ラプラス変換を学ぶ
2022年11月に発売された【手を動かしてまなぶシリーズ】のフーリエ解析・ラプラス変換を教科書とした講義です.
【手を動かしてまなぶシリーズ】らしく,例題を中心とした構成となっており,問題を解きながら理論とその概念が必要なモチベーションを理解することができます.
※アーカイブ講座の動画販売についてお申し込み受付中です。
数学講座
通常講座
Sスタンダード
アーカイブ講座(録画販売中)
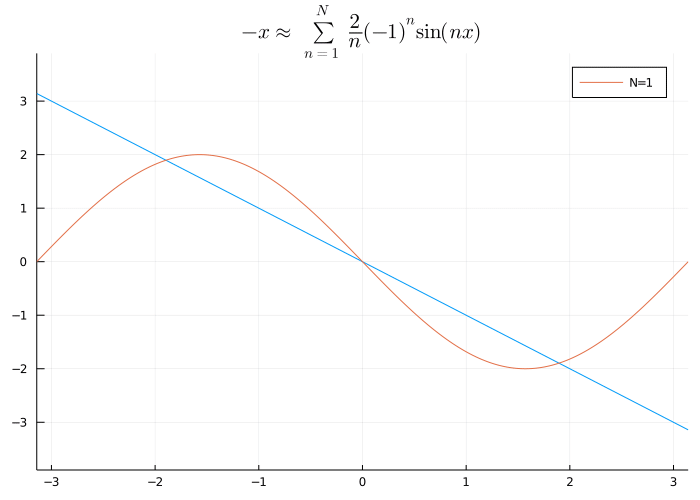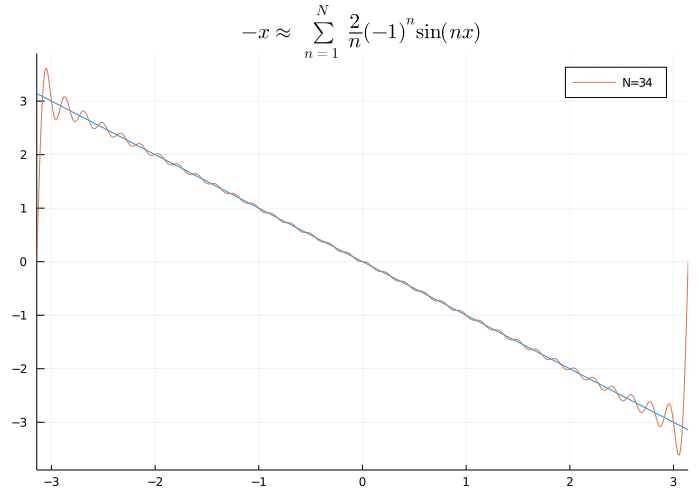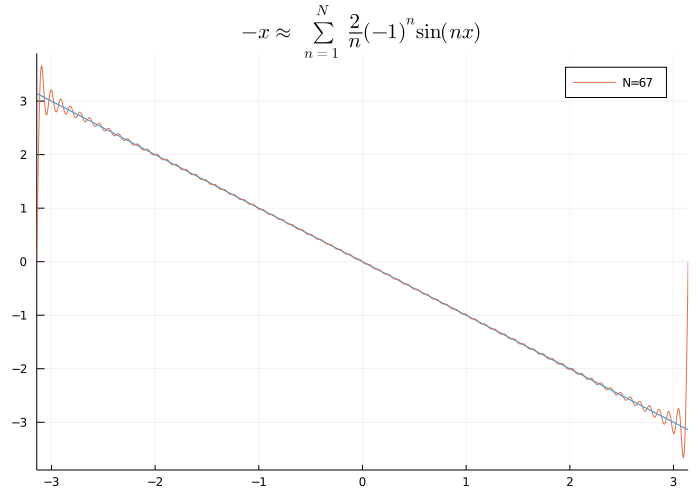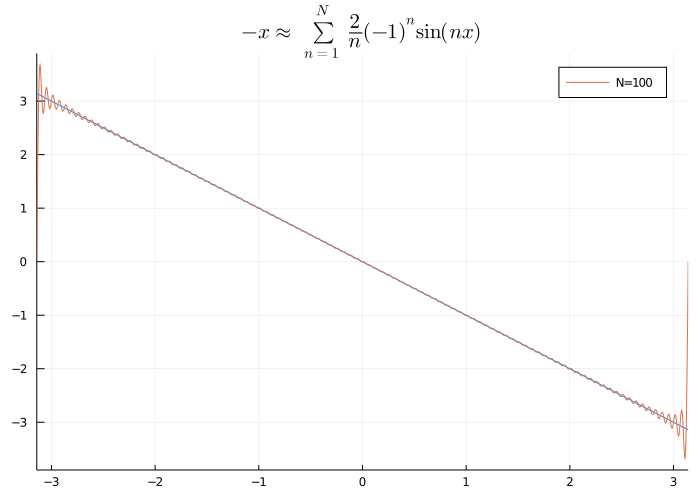
2022年11月に発売された【手を動かしてまなぶシリーズ】のフーリエ解析・ラプラス変換を教科書とした講義です.
【手を動かしてまなぶシリーズ】らしく,例題を中心とした構成となっており,問題を解きながら理論とその概念が必要なモチベーションを理解することができます.
※アーカイブ講座の動画販売についてお申し込み受付中です。
ジョセフ・フーリエ(Joseph Fourier, 1768-1830)は物体の熱の伝わり方に関する研究から「周期関数\(f\)を三角関数(\(\sin\), \(\cos\))の和で
\begin{align*}
f(x)=c+\sum_{n=1}^{\infty}(a_{n}\sin{nx}+b_{n}\cos{nx})
\end{align*}
と近似する」という手法を考えました.現代では,この三角関数の和をフーリエ級数といいます.

\(f(x)=-x\)の\(-\pi\le x\le\pi\)でのフーリエ級数展開
物理的には\(\sin\), \(\cos\)は「波」を表すことから, フーリエ級数は関数を周波数を用いて表すものという側面を持ちます.
このフーリエ級数に始まる分野はフーリエ解析と呼ばれ,フーリエ級数の他にフーリエ変換
\begin{align*}
\widehat{f} (\xi)=\frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}}f(x)e^{-i\xi x}\,dx
\end{align*}
もフーリエ解析に含まれます.
また,フーリエ変換と似たラプラス変換もフーリエ解析と同様に広く応用されています.

山根 英司 著『手を動かしてまなぶ フーリエ解析・ラプラス変換』裳華房を教科書として使用します。
山根英司
裳華房
ラプラス変換は常微分方程式を,フーリエ解析は偏微分方程式を解く際に便利なことも多いです.
そこで本講座では微分方程式を解くことを目標にラプラス変換・フーリエ解析を学んでいきます.
授業中にも予備知識を復習をしますが,微分積分学の既習を仮定します.
また,簡単な微分方程式の知識を知っていると見通しよく学べますが,こちらは必須ではありません.
ラプラス変換は関数を別の関数に変換する操作のひとつです.
ラプラス変換を用いると,例えば
\begin{align*}
y^{\prime\prime}(t)-y^{\prime}(t)-6y(t)=e^t\quad(t\in\mathbb{R})
\end{align*}
といった常微分方程式に初期条件
\begin{align*}
y(0)=1,\ y'(0)=2
\end{align*}
を課した初期値問題を簡単に解くことができます.
ここでは常微分方程式の初期値問題への応用を目標に,ラプラス変換の考え方・基本性質を紹介します.
ラプラス変換と同様に,フーリエ変換も関数を別の関数に変換する操作のひとつです.
フーリエ変換を用いると,例えば
\begin{align}
\frac{\partial u}{\partial t}(x,t)-\frac{\partial^2u}{\partial x^2}(x,t)=0\quad(t>0,x\in\mathbb{R})
\end{align}
といった偏微分方程式に初期条件
\begin{align*}
u(x,0)=f(x)
\end{align*}
を課した初期値問題の(形式的な)解を見つけることができます.
なお,この偏微分方程式は熱(伝導)方程式と呼ばれており,時間経過による熱の伝わり方を表す偏微分方程式として良く知られています.
ここでは空間\(\mathbb{R}\)上の偏微分方程式の初期値問題への応用を目標に,フーリエ変換の考え方・基本性質を紹介します.
フーリエ級数は関数を\(\sin\), \(\cos\)の和で近似した級数のことです.
フーリエ級数を用いると,例えば
\begin{align}
\displaystyle\frac{\partial^2 u}{\partial t^2}(x,t)-\frac{\partial^2u}{\partial x^2}(x,t)=0\quad(t>0,0\le x\le\pi)
\end{align}
といった偏微分方程式に初期条件
\begin{align*}
u(x,0)=f(x),\ \frac{\partial u}{\partial t}(x,0)=g(x)
\end{align*}
と境界条件
\begin{align*}
u(0,t)=u(\pi,t)=0
\end{align*}
を課した初期値境界値問題の(形式的な)解を見つけることができます.
なお,この偏微分方程式は波動方程式と呼ばれており,時間経過による波の伝わり方を表す偏微分方程式として良く知られています.
ここでは有界区間上の偏微分方程式の初期値・境界値問題への応用を目標に,フーリエ変換の考え方・基本性質を紹介します.
| 講座名 | 手を動かしてまなぶ フーリエ解析・ラプラス変換 |
|---|---|
| 担当講師 | |
| 開講スケジュール |
土曜クラス : 10:00-12:00
2023年4月8日~2023年8月26日
4月29日、8月12日土曜日は休講です。 |
| 受講方法 |
Zoomによるオンライン講座 |
| 教科書 | 山根 英司 著『手を動かしてまなぶ フーリエ解析・ラプラス変換』裳華房 ※著作権の関係上、お持ちでない場合は必ずご購入いただくようお願いいたします。著者及び出版社には、教科書として使用する許可を得ておりますが、本講座とは無関係です。 本講座に関しては弊社へのみお問い合わせください。 |
| 受講料 | 税込19,500円/月(税込97,500円/5ヶ月一括) |
| お支払い方法 |
クレジットカード支払いは本ページ下部「受講料のお支払いについて」よりお願いいたします。 |
| 準備物 | 筆記用具と教科書 |
| その他 | 初回講義での体験受講が可能です。 |
下記のボタンを押すと該当する集団講座のチケットをご購入いただけます。
※ボタンを押すと、stripeの決済ページへ遷移します。

| 1ヶ月 | 2ヶ月 | 5ヶ月一括 |
|---|---|---|
2020年前期分よりオンライン授業を録画し、授業の録画販売(アーカイブ販売)を行っております。



アーカイブ講座の動画購入をご検討いただく場合は、下記についてご確認をお願いいたします。
本講座は開講中の講座はございません。
アーカイブ講座(録画購入)にてご受講いただけます。
アーカイブ講座(録画購入)のお申し込みはこちら
| 講座名 | 動画内容 | 講師名 | 受講料 |
|---|---|---|---|
| 手を動かしてまなぶ フーリエ解析・ラプラス変換 2023年前期 |
全19回 (各120分) |
山本 拓人 | 19,500円/月(97,500円/5ヶ月一括) |
年度別 講座情報
| 年度 | 講座情報 |
|---|---|
| ー | 本講座は2023年前期のみの開講です。 |
講座のお申し込み・ご相談は
気軽にお問い合わせください。