
大学数学のスタート地点
理工系の大学生ならば1年次に必ず学ぶことになる線形代数を、初歩から丁寧に学びます。
大学数学を学び始める方はもちろん、AI技術を含む情報科学に興味をお持ちの方にもスタート地点として最適な講座です。
初めて学ぶ方にも学び直したい方にも、線形代数の基礎理論を豊富な具体例を交えながらわかりやすく解説いたします。
※2024年10月のご受講についてお申し込み受付中です。
数学講座
通常講座
Sスタンダード
開講中
アーカイブ講座(録画販売中)

理工系の大学生ならば1年次に必ず学ぶことになる線形代数を、初歩から丁寧に学びます。
大学数学を学び始める方はもちろん、AI技術を含む情報科学に興味をお持ちの方にもスタート地点として最適な講座です。
初めて学ぶ方にも学び直したい方にも、線形代数の基礎理論を豊富な具体例を交えながらわかりやすく解説いたします。
※2024年10月のご受講についてお申し込み受付中です。
このページをご覧になっている方は、数学になんらかの形でご興味をお持ちのことと思います。高校数学をもう一度学び直そうとお考えの方や、微分・積分の理論から発展する解析学、図形の性質を分析する幾何学、方程式や数の扱いを追求する代数学などのいわゆる「大学数学」に関心をお寄せの方も多いでしょう。また、統計学や確率論、データサイエンスなどの応用数学が、AI技術の発展も相まって、社会でますます存在感を高めていることもご承知の通りです。ここには書ききれないほどに分化および先鋭化しつつある数学のあらゆる分野の、ほとんどすべてに応用を持つ基礎理論を挙げるとするならば、それが線形代数に他なりません。
線形代数は文字通り、「線形性」と呼ばれる性質を持つ対象を研究する分野です。線形性は純粋数学のみならず、あらゆる理学、工学、情報学、社会科学が取り扱う現象に顔を出します。およそ理工系の大学生ならば、ほとんど確実に1年次の必修科目として線形代数を履修することになる理由はここにあります。
線形性を研究するといっても、このままでは抽象的で、何から手をつけてよいものか途方に暮れてしまいます。このような線形性を持つ対象に、きわめて具体的な分析手法を与えるのが行列の理論です。線形代数の初級理論は、行列を用いて線形性を理解する方法論の集積であるともいえます。これらを駆使すると、抽象的で難解に思えたさまざまな問題を、単純な計算問題に帰着して解決してしまうことさえ可能なのです。実際、線形代数があらゆる分野で応用できるその根源は、この「計算問題にしてしまう力」によるところが大きいでしょう。
本講座では、現代のあらゆる科学技術の基礎のひとつである線形代数を、初歩の段階から丁寧に解説していきます。大学以降の数学を学ぶのに必須である集合と写像、論理の基本の解説も含むので、高校数学の初歩(数学I)程度の理解があれば受講することが可能ですし、高校数学から大学数学への橋渡しとしても最適です。
高校までの数学では、与えられた問題の解答を得るための《解法》が注目の対象であることが多いでしょう。しかし、大学以降の数学では具体的な問題の解法と並んで、上述のように難問をいかにして計算問題のような単純な問題に帰着させるか、その方法および《論理的な構造・プロセス》にこそ注目します。本講座における解説や議論を通じて、線形代数の基礎理論に習熟するとともに、生涯にわたって役にたつ、「数学的思考」をも身につけていただくことができるはずです。
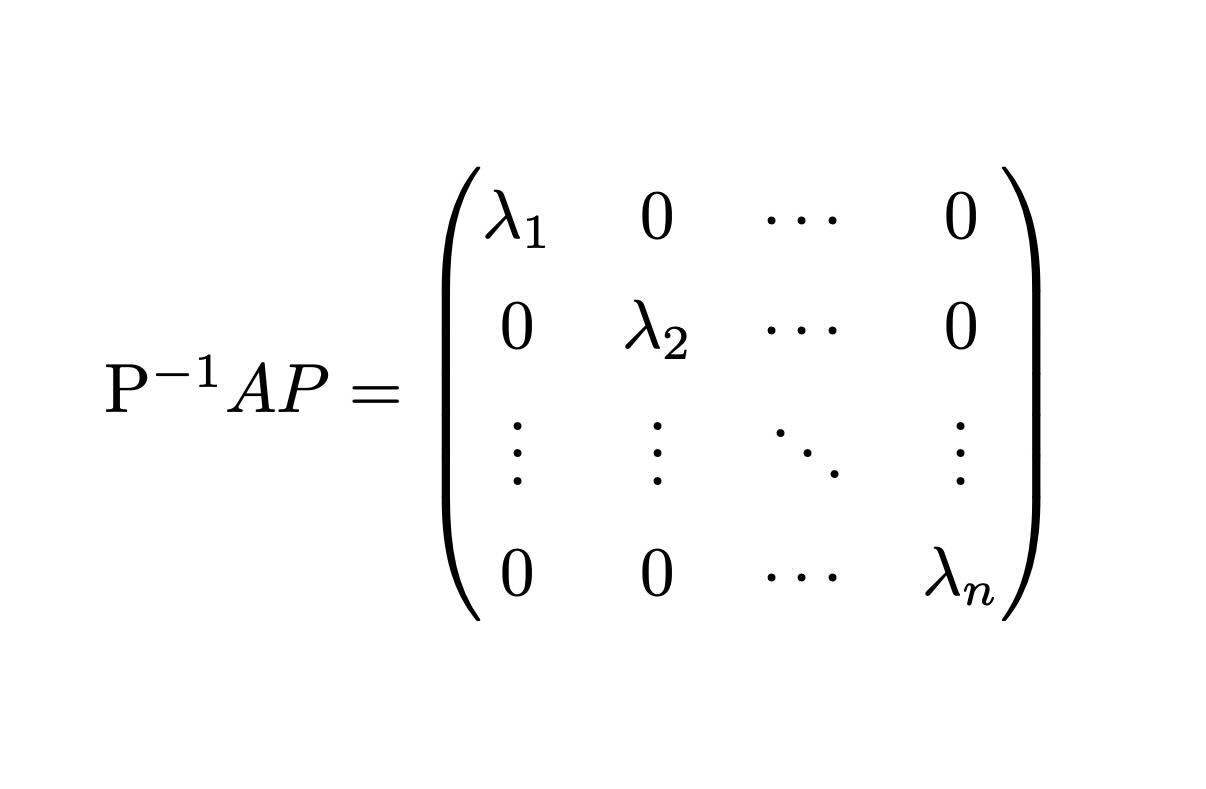

藤岡敦『手を動かしてまなぶ 線形代数』(裳華房)を教科書として使用します。
藤岡敦
裳華房
・行列の計算に習熟し、その意味を理解する
・ベクトル空間について理解し、行列の理論との関わりを学ぶ
・数学を学ぶ上で基礎となる集合や論理の取り扱いに親しみ、数学的思考の基本を身につける
高校数学の初歩(数学Iで学ぶ式の変形や方程式、関数の扱い)の理解があれば受講は可能です。
講義中に挙げる例や演習問題にはより発展的な題材が含まれることがあります。数学A、II、B、III、Cの知識があればより深い理解につながりますが、受講生の皆さまの前提知識に合わせ、講義中に適宜解説を行います。その他大学数学の知識は不要です。
線形代数の理論の根幹をなす行列の取り扱いについて学びます。行列および関連する用語の定義、行列の演算、逆行列などについて解説します。
連立一次方程式を行列によって表し、解を求める方法について学びます。行列の基本変形、掃き出し法、行列の階数などについて解説します。
行列の性質を反映した数値である行列式について学びます。置換、行列式の定義と性質、行列式の計算方法、行列式の展開、外積、行列式の幾何学的意味などについて解説します。
行列の指数関数およびその性質について学びます。マクローリン展開、行列の指数関数について解説します。
線形代数における最重要概念のひとつ、ベクトル空間について学びます。ベクトル空間および関連用語の定義、ベクトル空間の例、性質、1次独立・従属、ベクトル空間の基底、生成、次元などについて解説します。
ベクトルや行列、ベクトル空間の理論は、線形写像を理解する方法論であるといえます。写像の基礎からはじめ、線形写像の意味と取り扱いについて学びます。集合と写像、線形写像の定義、像と核、線形写像の表現行列などについて解説します。
線形写像の統一的な理解に欠かせない概念である固有値と固有ベクトルについて学びます。固有値と固有ベクトルの定義、その計算方法、ケイリー・ハミルトンの定理などについて解説します。
線形写像は行列を用いて表現できますが、その際なるべく「易しい」行列を用いたくなるのは自然なことでしょう。与えられた行列を、そのような易しい行列の最たる例である対角行列に近付けていく、行列の標準化の問題について学びます。行列の対角化、対角化可能性、その応用について解説します。
ベクトル空間に内積という構造を与え、ベクトルを計量するさまざまな手法を学びます。内積、内積空間、ノルム、正規直交基底、グラム・シュミットの直交化法、直交行列などについて解説します。
対称行列は直交行列を用いて対角化することができます。その理論的な側面および具体的な計算手法について学びます。対称行列、エルミート内積、対称行列の固有値が実数であること、対称行列が直交行列で対角化可能であることなどについて解説します。時間の許す限り、さまざまな応用についても触れます。
| 講座名 | 線形代数入門 |
|---|---|
| 担当講師 |
赤澤涼
|
| 開講スケジュール |
土曜クラス:10:00-12:00 |
| 受講方法 |
Zoomによるオンライン講座 授業は録画されます。録画(アーカイブ動画)は授業終了から5年間オンラインにて繰り返しご視聴いただけます。(ダウンロード不可) 詳細はこちらのページをご確認ください。 |
| 教科書 | 藤岡敦『手を動かしてまなぶ 線形代数』(裳華房) |
| 受講料 | 税込19,500円/期(税込97,500円/5期一括) |
| お支払い方法 |
クレジットカード支払いは本ページ下部「受講料のお支払いについて」よりお願いいたします。 |
| 準備物 | Zoomで受講するためのPC |
| その他 | 初回講義での体験受講が可能です。 |
下記のボタンを押すと該当する集団講座のチケットをご購入いただけます。
※ボタンを押すと、stripeの決済ページへ遷移します。

| 1期分 | 2期分 | 5期一括 |
|---|---|---|
2020年前期分よりオンライン授業を録画し、授業の録画販売(アーカイブ販売)を行っております。



アーカイブ講座の動画購入をご検討いただく場合は、下記についてご確認をお願いいたします。
本講座は開講中の講座はございません。
アーカイブ講座(録画購入)にてご受講いただけます。
アーカイブ講座(録画購入)をご希望の場合はこちらからお申込みください。
| 講座名 | 動画内容 | 講師名 | 受講料 |
|---|---|---|---|
| 線形代数入門 2022年前期 |
全19回 (各120分) |
山本 拓人 | 19,500円/期(97,500円/5期一括) |
| 線形代数入門 2021年後期 |
全19回 (各120分) |
山本 拓人 | 19,500円/期(97,500円/5期一括) |
| 線形代数入門 2021年前期 |
全19回 (各120分) |
神戸祐太 |
19,500円/期(97,500円/5期一括) |
| 線形代数入門 2020年後期 |
全19回 (各120分) |
中村 伸一郎 | 19,500円/期(97,500円/5期一括) |
年度別 講座情報
| 年度 | 講座情報 |
|---|---|
| 2023年前期 | 教科書:加藤文元著『数研講座シリーズ 大学教養 微分積分』数研出版 |
| 2022年前期 | |
| 2021年後期~2020年後期 |
講座のお申し込み・ご相談は
気軽にお問い合わせください。