高校数学の集大成!【極限・微分・積分・ベクトル・複素数】
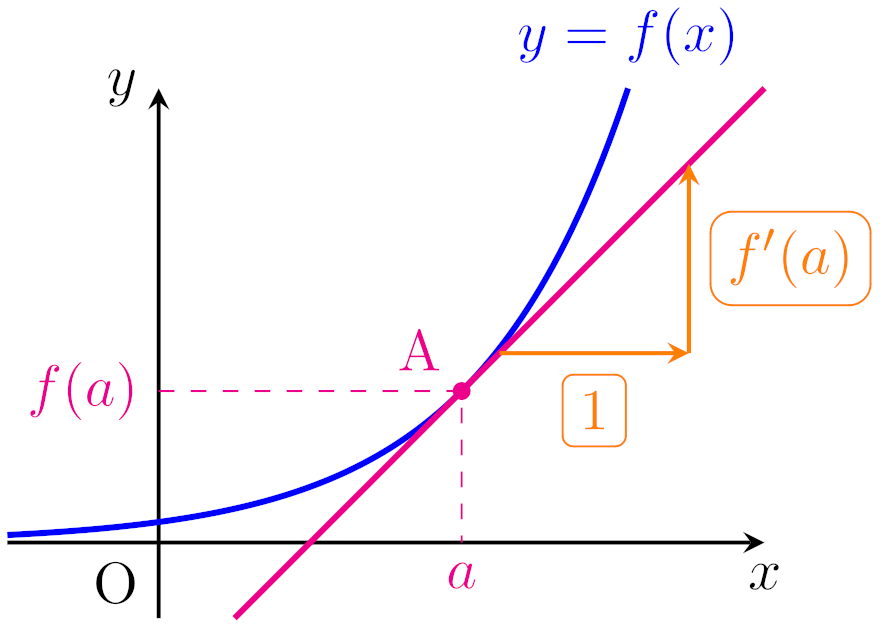
高校数学の「数学III」では様々な関数の極限・微分・積分を学びます.これらは互いに密接に関係しており,これらを学ぶことで「数学IIまでに学んだ様々な関数を併せた複雑なグラフを描く」「平面図形の面積・空間図形の体積を求める」といったことができるようになります.
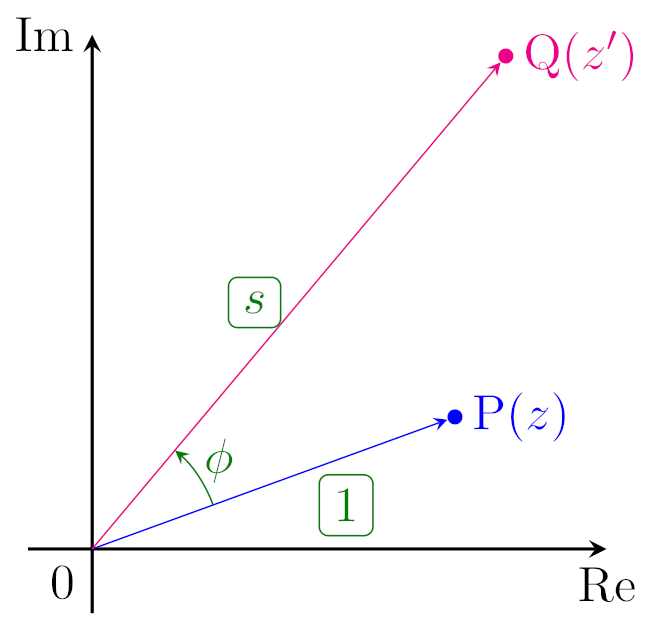
高校数学の「数学C」ではベクトル・複素数を学びます.ベクトルも複素数を学ぶことで「図形上の2点の関係性を理解する」といったことができるようになり,複雑な図形でも機械的な計算で捉えられることが多くなります.
※アーカイブ講座の動画販売についてお申し込み受付中です。